Recently I trained a policy to play Breakout, a classic game commonly used as a benchmark in reinforcement learning (RL). The goal of the game is to break as many bricks as possible, without letting the ball hit the bottom of the screen.

To evaluate the average return (score) of the policy, I ran the policy for 128 episodes (games*) and calculated the average score. However, this can be pretty slow since a single episode of Breakout can take minutes to complete. To speed things up, I used EnvPool, a vectorized environment wrapper.
Vectorized environments are popular for speeding up both training and evaluation in RL: they run
multiple environments in parallel, with steps happening in unison. This behavior is
usually wrapped into a single batched step(...) function that receives a batch of
actions and returns a batch of observations:
batch_actions = policy(batch_obs)
batch_next_obs, batch_rewards, batch_dones, info = vectorized_env.step(batch_actions)
The vectorized environment will also typically handle the logic of resetting each environment to a new episode once the previous episode has ended.
My first approach was to run the policy in the vectorized environment until a total of 128 episodes have been played, and then to stop and calculate the average return. In code, that looks something like:
episode_returns = []
batch_obs = vectorized_env.reset()
while len(episode_returns) < NUM_EVALS:
batch_actions = policy(batch_obs)
batch_obs, _, batch_dones, info = vectorized_env.step(batch_actions)
for i in range(NUM_ENVS):
# Check if episode in environment i has ended
if batch_dones[i] and len(episode_returns) < NUM_EVALS:
# Record the return (score) of the episode
episode_returns.append(info["final_return"][i])
In principle, parallelization should get you the same result in less time. But a surprising result of this implementation is that the reported return changes as you increase the amount of parallelization. In this case, the reported return decreases by around 150 as you go from 1 to 128 parallel environments:
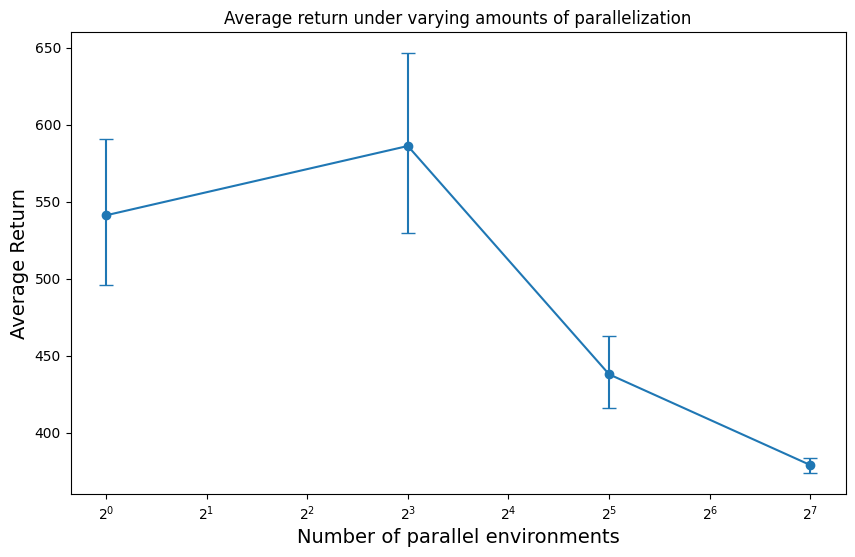
The culprit becomes clearer when we look at how average episode length changes as we increase parallelization:
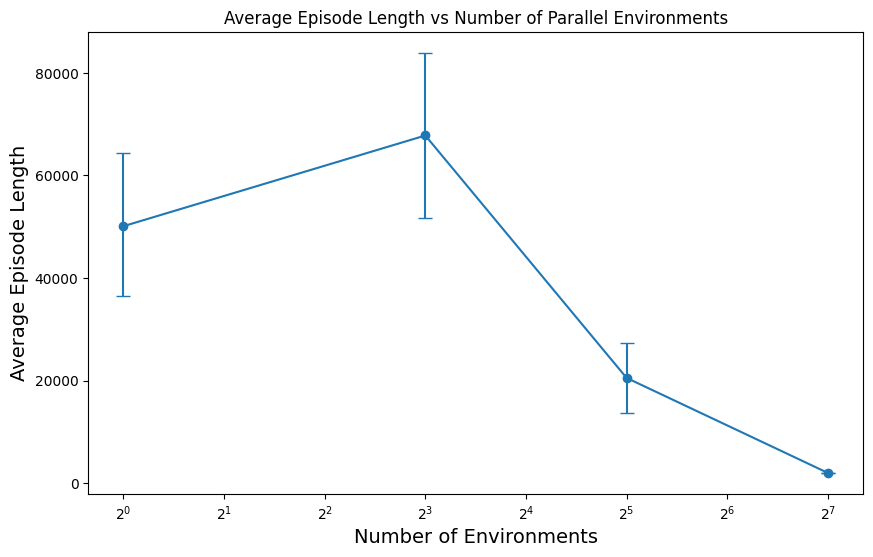
This plot looks almost identical to the return plot above, but it’s measuring the number of steps instead of the score. This is not surprising: Breakout is a game where it takes more time to break more bricks and achieve a higher score, so we expect a strong correlation between return and episode length.
But what the plot shows is that parallelization creates a bias towards shorter episodes. Environments that happen to have shorter episodes finish more quickly, meaning more of them get counted towards the final average.
The straightforward fix is to run each of the environments until it has played the same number of episodes. With this implementation, the reported average return does not decrease as we increase parallelization:
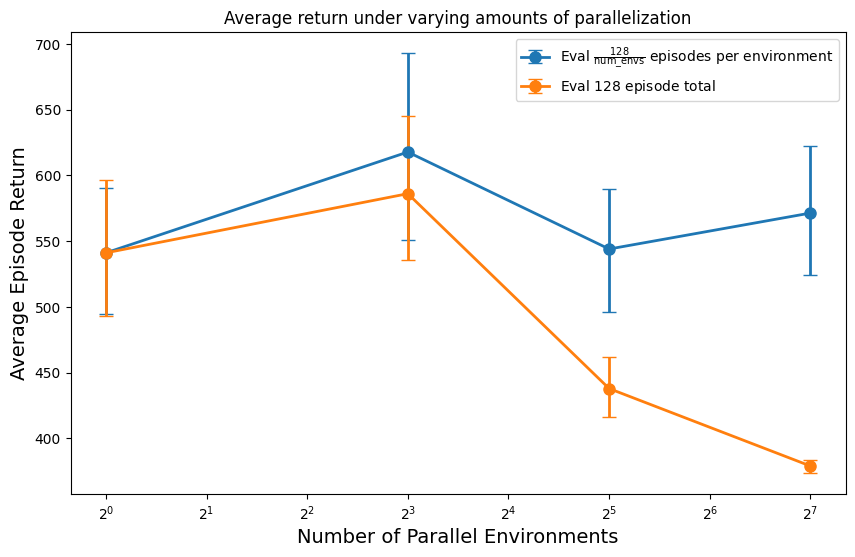
This problem and its solution are not new: the Stable Baselines3 library, for example, identified this issue and implemented a similar solution. But researchers often prefer independent single-file re-implementations of RL algorithms rather than large unified libraries, since they are easier to understand and modify. Evaluation seems simple enough to implement yourself, but like many things in RL, can be tricky to get right.