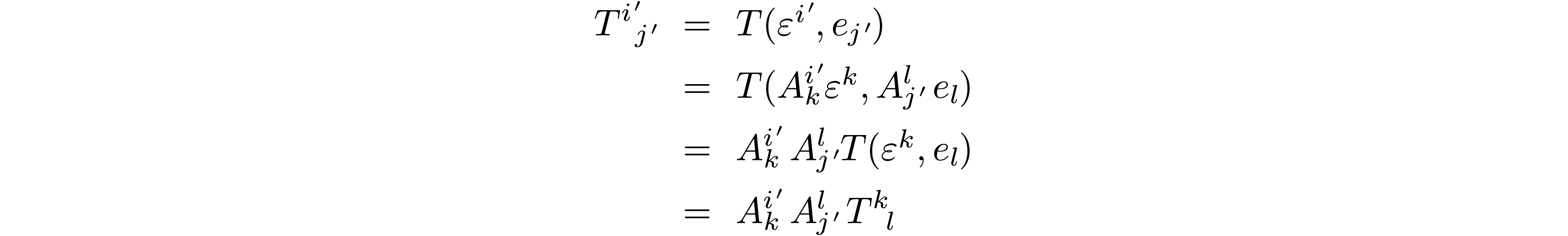This book [1] uses an interesting notation for change of basis calculations where the two bases are distinguished by priming the indices.
Suppose for some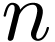 
-dimensional vector space 
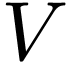we have an original basis 
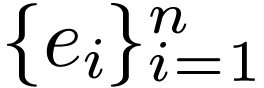and a primed basis 
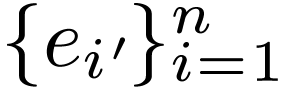(of course, the choice
of calling one basis the original the other primed is arbitrary). There
are linear transformations from each basis to the other:
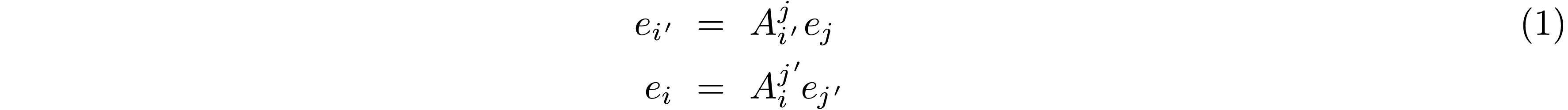
Note that the position of the prime matters: if we consider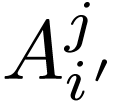 
and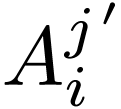 
as matrices, they would be two
different matrices. In fact, they would be inverses. Using the
fact that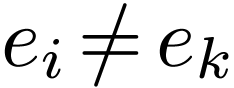 
for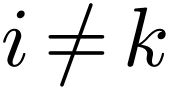 
:
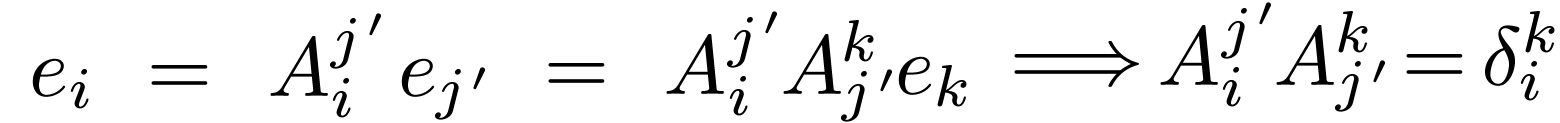
How does the dual basis transform between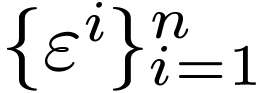 
and
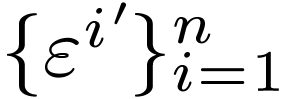? Since each 
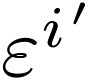is itself a
covector, we can express it in terms of its components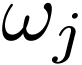 
in the original dual basis:
 |
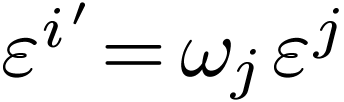(2) |
Then we determine what the 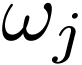are by
evaluating 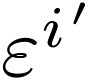on the basis vectors:
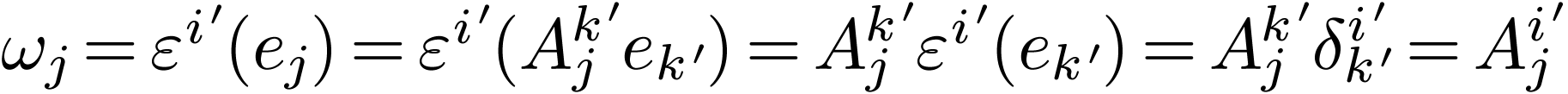
Plugging this result back into Eq 2 we get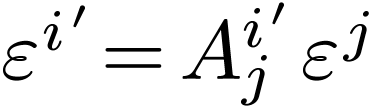 
.
A similar calculation gives the opposite change of dual basis:
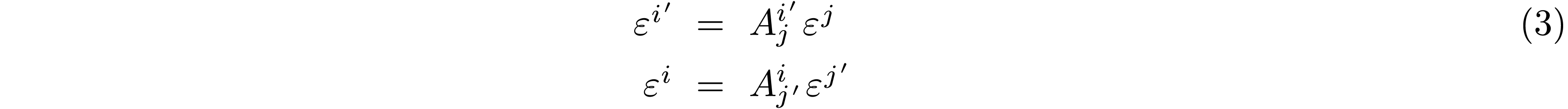
Comparing this to Eq. 1, we see that the dual basis changes in the inverse manner as the basis.
For a vector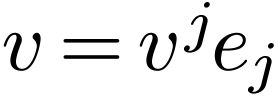 
, how do the vector components 
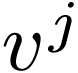change from the original to primed basis? Recall that
we can use the 
'th dual basis to obtain the 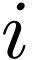'th component of a vector:
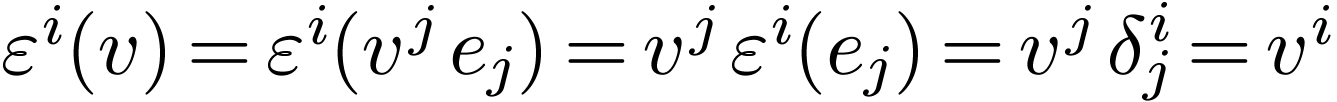
and similarly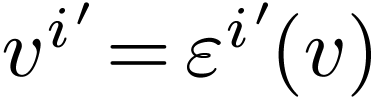 
. Expanding
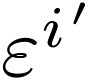using Eq. 3:
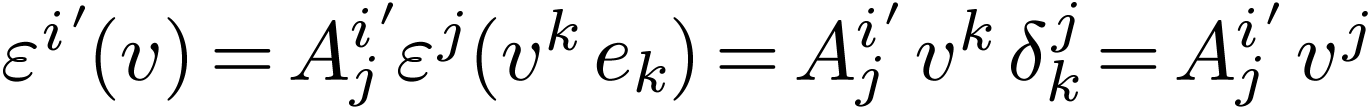
So (after a similar calculation in the opposite direction) we see vector components change as:
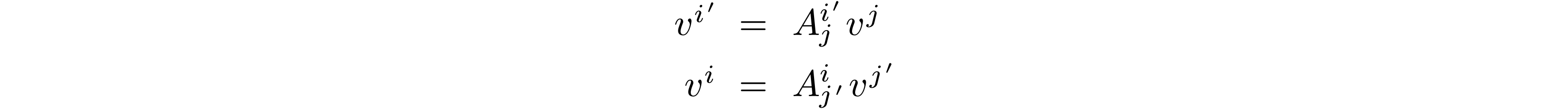
Now consider a (1,1)-tensor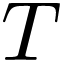 
with components 
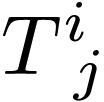in the original basis. Unlike the book we use the
convention that a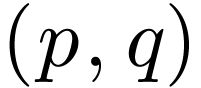 
-tensor
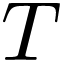is a multilinear map:
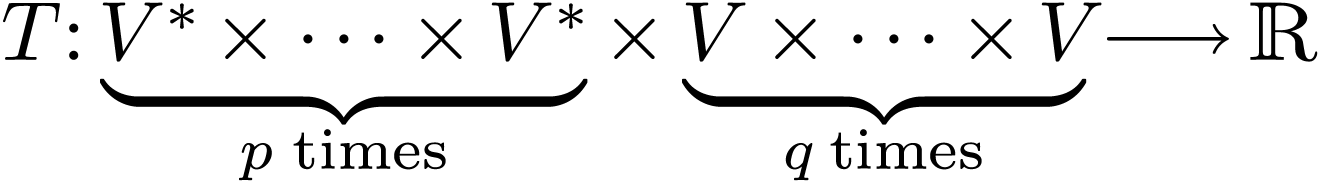
How do the tensor components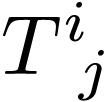 
transform from the
original to primed basis? We can simply evaluate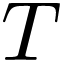
on the primed basis and expand:
